Research Projects
Knowledge does not come, but you have to go to it
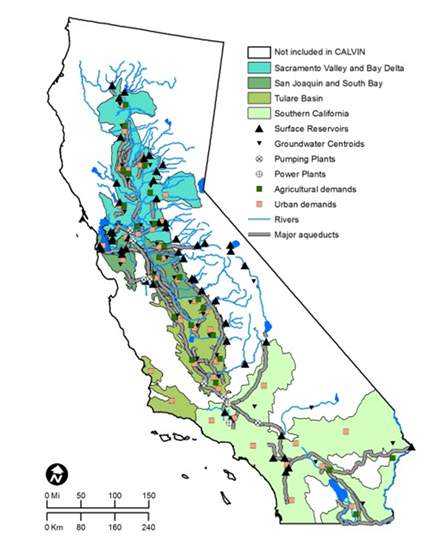
Modeling the Hydropower Systems of the Primary Tributaries of California's San Joaquin River
Mohammed Aburidi, Gustavo Facincani, David Rheinheimer, and Josh Veries
This project focuses on simulating and optimizing the hydropower systems of the primary tributaries of California’s San Joaquin River, including the Merced, San Joaquin, Stanislaus, and Tuolumne Rivers. These rivers play a critical role in California’s water management and energy production. Using the Pywr framework, we developed a detailed computational model to simulate water flow, reservoir operations, and energy generation across these interconnected systems. The model accounts for key operational constraints, such as water demand, environmental flow requirements, and energy production targets, providing insights into sustainable hydropower operations. Our work aims to enhance the understanding of hydropower dynamics within the region while supporting decision-making processes for water resource management, energy optimization, and ecological preservation.
Read less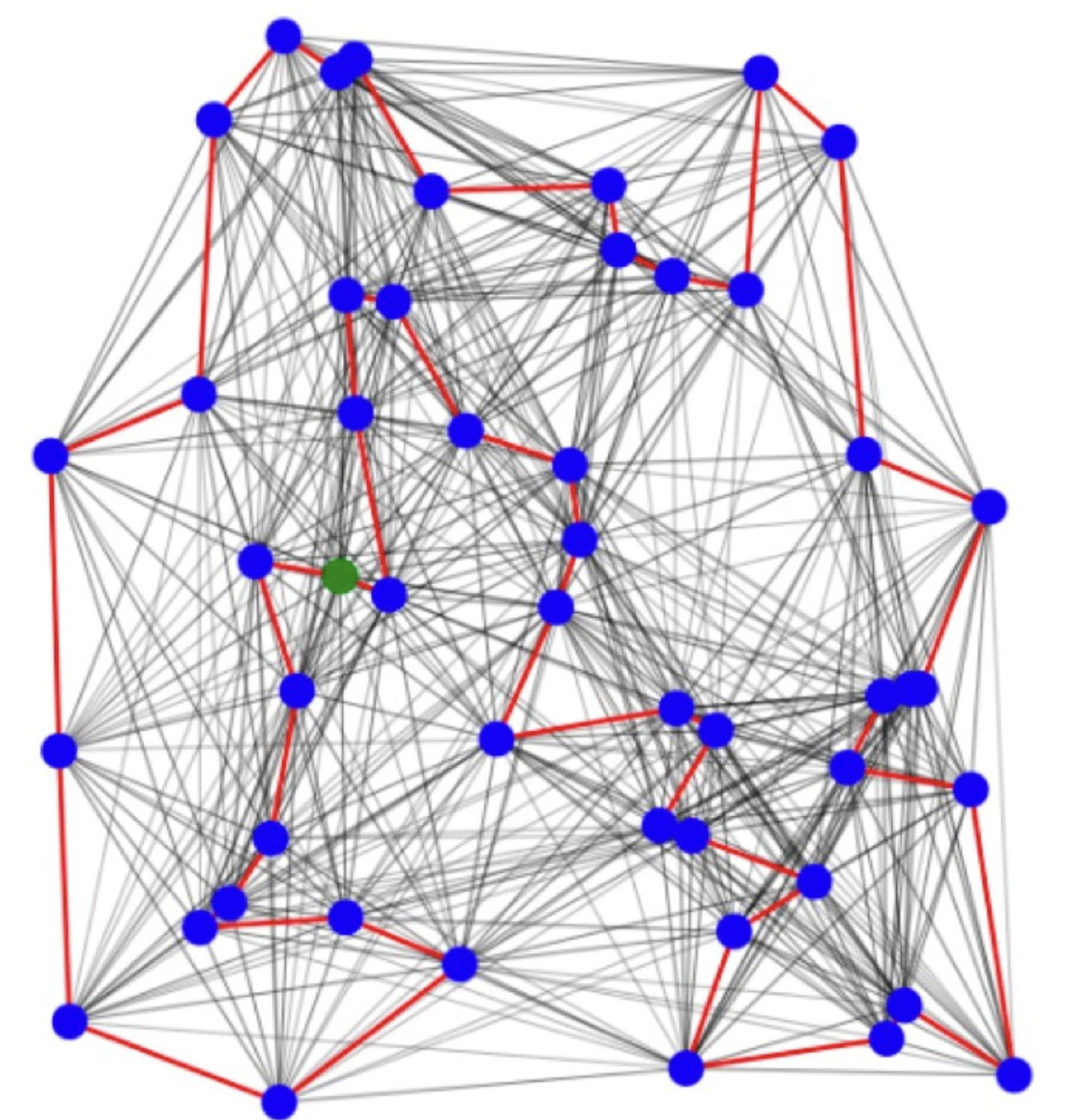
Graph Neural Networks (GNNs) have exhibited remarkable success in various applications, yet their vulnerability to adversarial attacks poses significant risks in security-sensitive domains. Imperceptible perturbations in graphs can lead to severe performance degradation, necessitating robust GNN models for safety and privacy in critical applications. We address this challenge by proposing optimization-based attacks on GNNs, specifically focusing on modifying graph structures. Our approach leverages convex relaxation and projected momentum optimization. Introducing the focal loss as an attack criterion, we generate perturbations by minimizing a constrained optimization problem.
Read less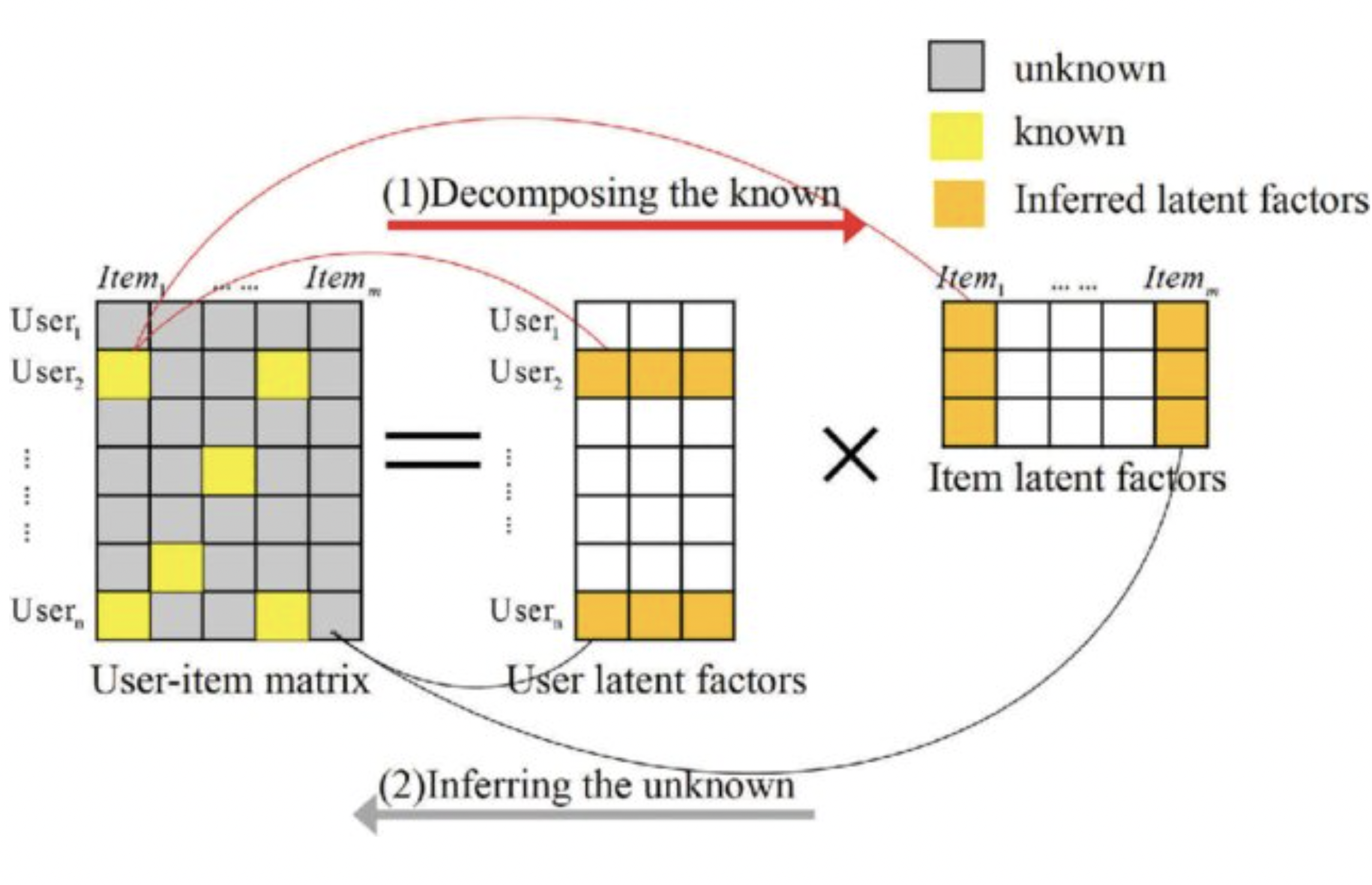
Drug-Drug Interaction Prediction via Matrix Factorization
Mohammed Aburidi and Roummel Marcia
Optimization plays a pivotal role in addressing real-life problems by providing systematic and efficient methods to find the best possible solutions amid various constraints. In this project,my contribution centers on the development of optimization techniques to predict the drug drug interactions. By mathematically formulating the problem as a matrix factorization and employing or devising algorithms to identify optimal solutions, we optimize and enhance drug efficiency, reduces side effects and costs, and maximizes desired outcomes.
In this research endeavor, I focus on harnessing the capabilities of matrix factorization as a robust mathematical framework for modeling intricate systems in real-world scenarios, focusing on drug-drug interactions. The focal point of my investigation lies in the application of similarity-constrained matrix factorization to predict Drug-Drug Interactions. We start our methodology by first calculating drug similarities and Gaussian interaction profile for each drug pair. We then apply matrix factorization on DDI interaction matrix and estimate the latent matrices constrained by the similarities. This approach will effectively map data from a high-dimensional space to a lower-dimensional space (i.e. latent space). Recent studies underscore the significance of this mapping, as it preserves topological data, yielding enhanced features \cite{chen2018algorithm}. This projection offering profound insights into DDIs. This mathematical endeavor transforms into a constrained optimization problem. Whereas different similarity constraints can be integrated such as drug substructure, targets, side effects, off-label side effects, and pathways, along with Gaussian interaction profiles for drug pairs. Newton’s method could be chosen as an optimization solver for optimizing the latent matrices A and B, and unraveling the intricate mathematical landscape underlying the optimization process. This research not only pushes the boundaries of matrix factorization applications but also underscores the pivotal role of mathematical optimization in elucidating complex interactions within drug systems.
Read less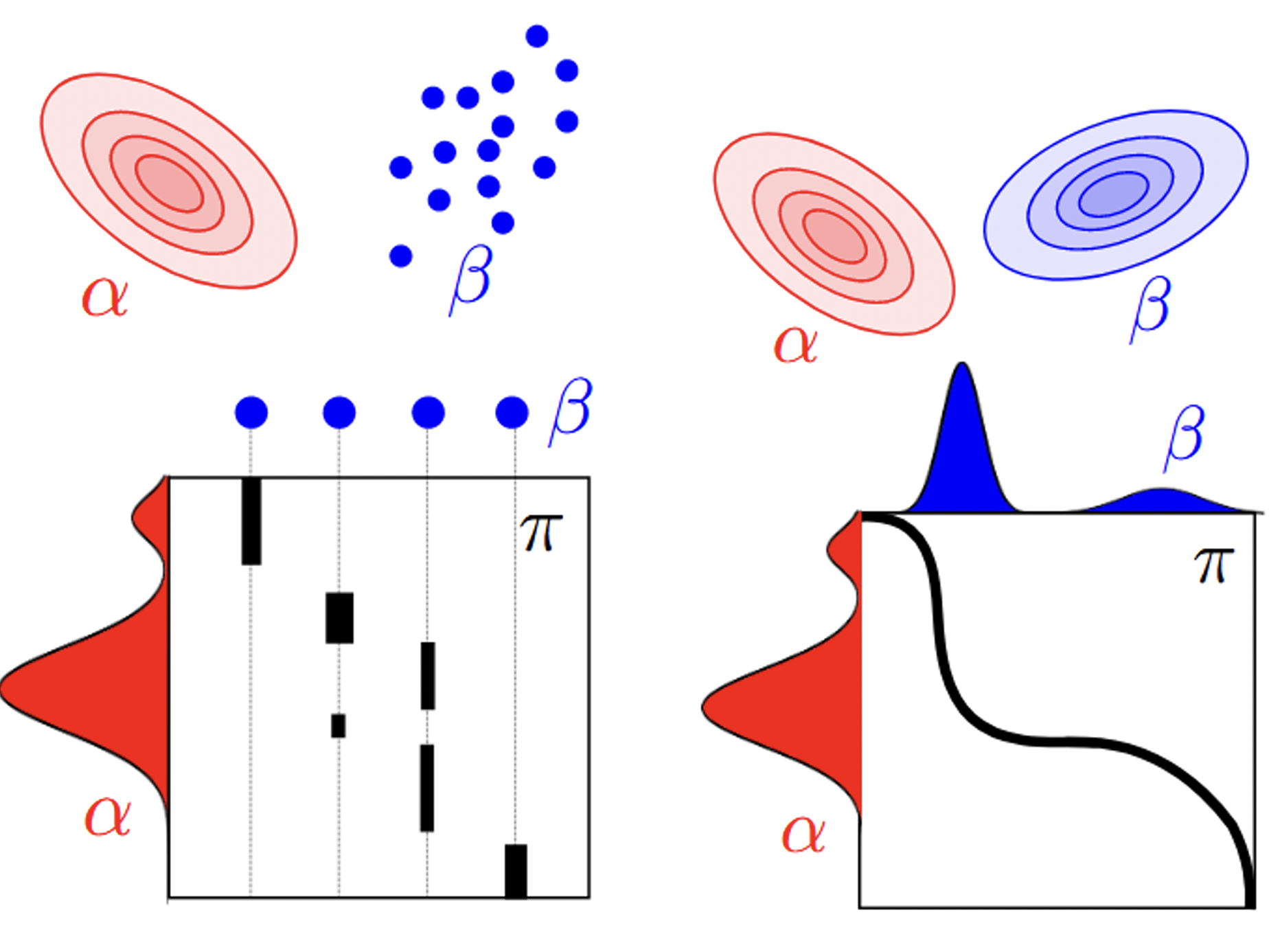
Optimal Transport-Based Network Alignment: Graph Classification of Small Molecule Structure-Activity Relationships in Biology
Mohammed Aburidi and Roummel Marcia
In the challenging world of early-stage drug development, where resources and data are limited, this project introduces a new way to improve predicting pharmaceutical properties. We’re focusing on optimizing the prediction of ADMET properties, which are crucial for understanding how drugs are absorbed, distributed, metabolized, and excreted in the body.
To predict ADMET properties. I first developed an optimal transport based distance metric fuse both Wasserstein and Gromov–Wasserstein distances \cite{peyre2017computational}, which I utilized to match the graphs and compute the similarities between every pair of drugs and to build a similarity matrix that is used in a graph kernel inputted into a learning algorithm.
I extended a new OT distance metric that is based on Wasserstein and Gromov–Wasserstein distances. The Wasserstein distance places a primary emphasis on the intrinsic features of graph elements (drug atoms), treating them in isolation, while the Gromov–Wasserstein distance directs its focus towards characterizing the relational aspects among these elements, elucidating the structural composition of the graph while excluding node features. The introduction of the new distance extends the capabilities of both Wasserstein and Gromov–Wasserstein distances by concurrently incorporating and harmonizing both feature and topological information, facilitating a comprehensive analysis of graph data. The resulting optimization problem is quadratic and solved using conditional gradient descent. We utilize it to compute the similarities between every pair of drugs and to build a similarity matrix that is used in a graph kernel inputted into a learning algorithm.
Read less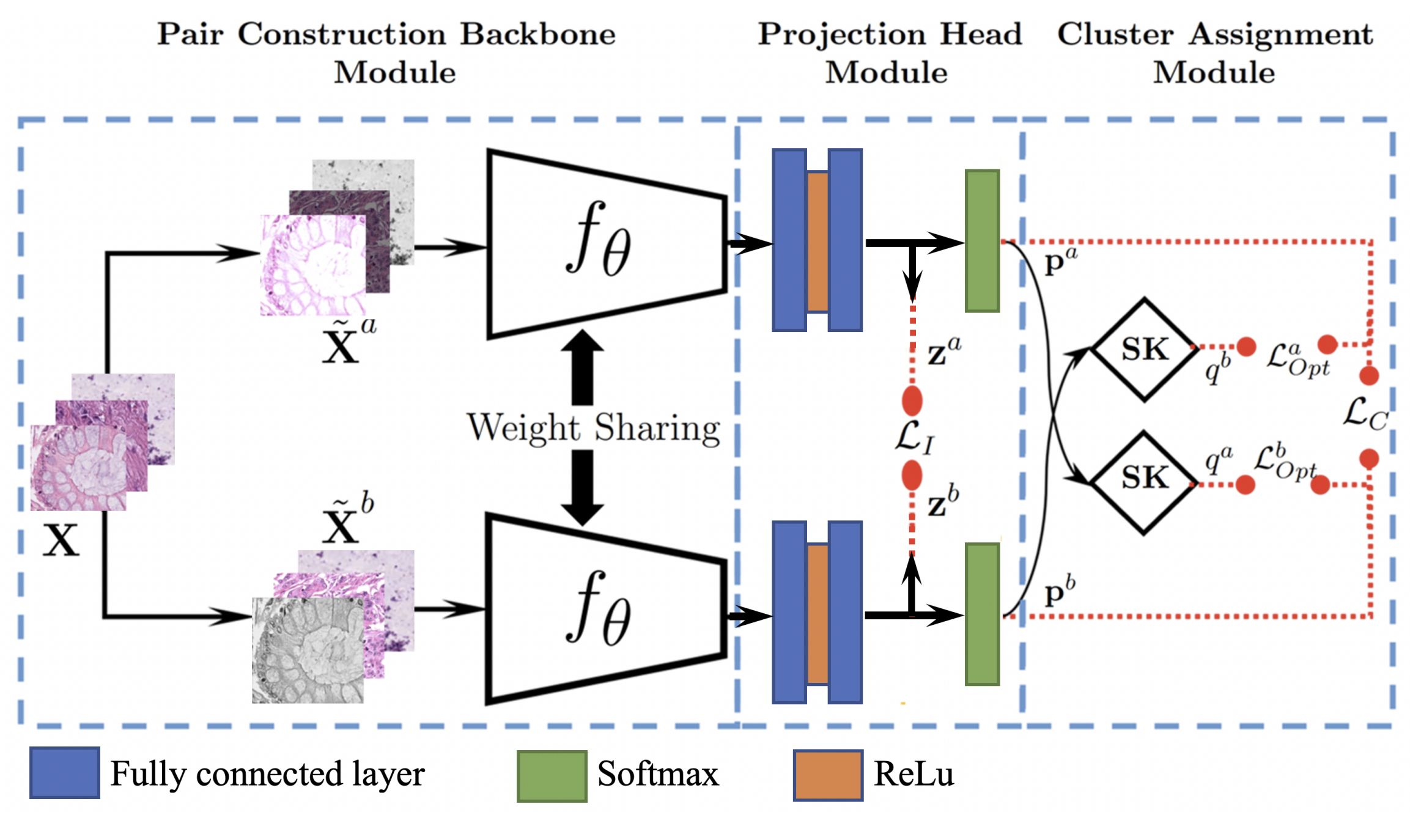
Optimal Transport and Contrastive-Based Clustering for Annotation-Free Tissue Analysis in Histopathology Images
Mohammed Aburidi and Roummel Marcia
L.
Read less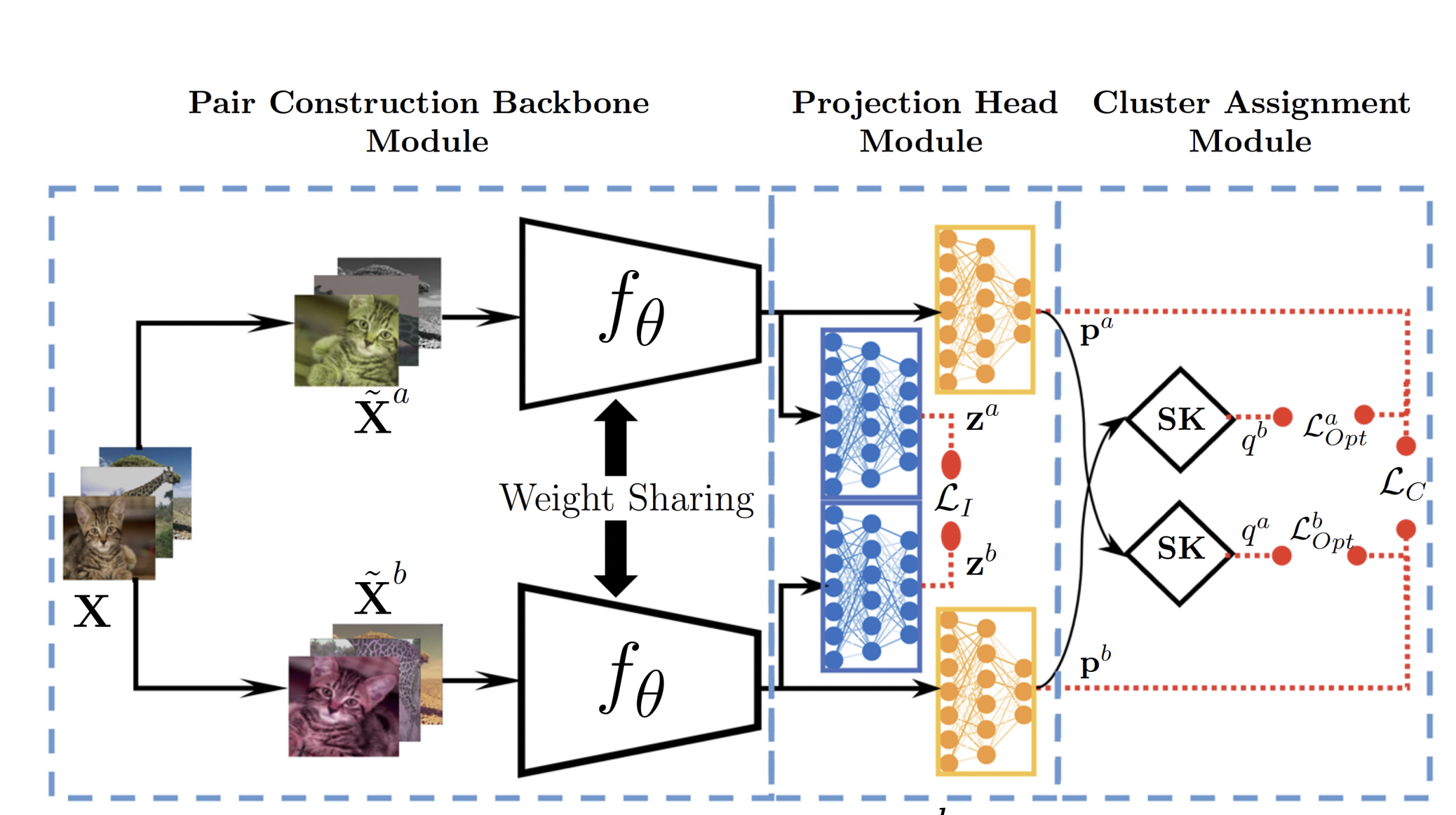
CLOT: Contrastive Learning-Driven and Optimal Transport-Based Training for Simultaneous Clustering
Mohammed Aburidi and Roummel Marcia
I proposed method, named CLOT (Contrastive Learning-Driven and Optimal Transport-Based Clustering) that employs robust and multiple-loss training and optimization settings. It is designed to derive artificial supervisory signals by solving the optimal transport optimization problem at the latent space and use them to self-label unlabeled images.
In the initial stage, CLOT employs instance- and cluster-level contrastive learning by maximizing similarities between projections of positive pairs (views of the same image) and minimizing those of negative pairs (views of other images). In the subsequent stage, it extends cross-entropy minimization to solve an optimal transport problem, using a fast Sinkhorn-Knopp algorithm to determine cluster assignments.
Our experiments demonstrate the superiority of CLOT over eight competitive clustering methods across challenging benchmarks, including CIFAR-100, STL-10, and ImageNet-10 for ResNet-34.
Read less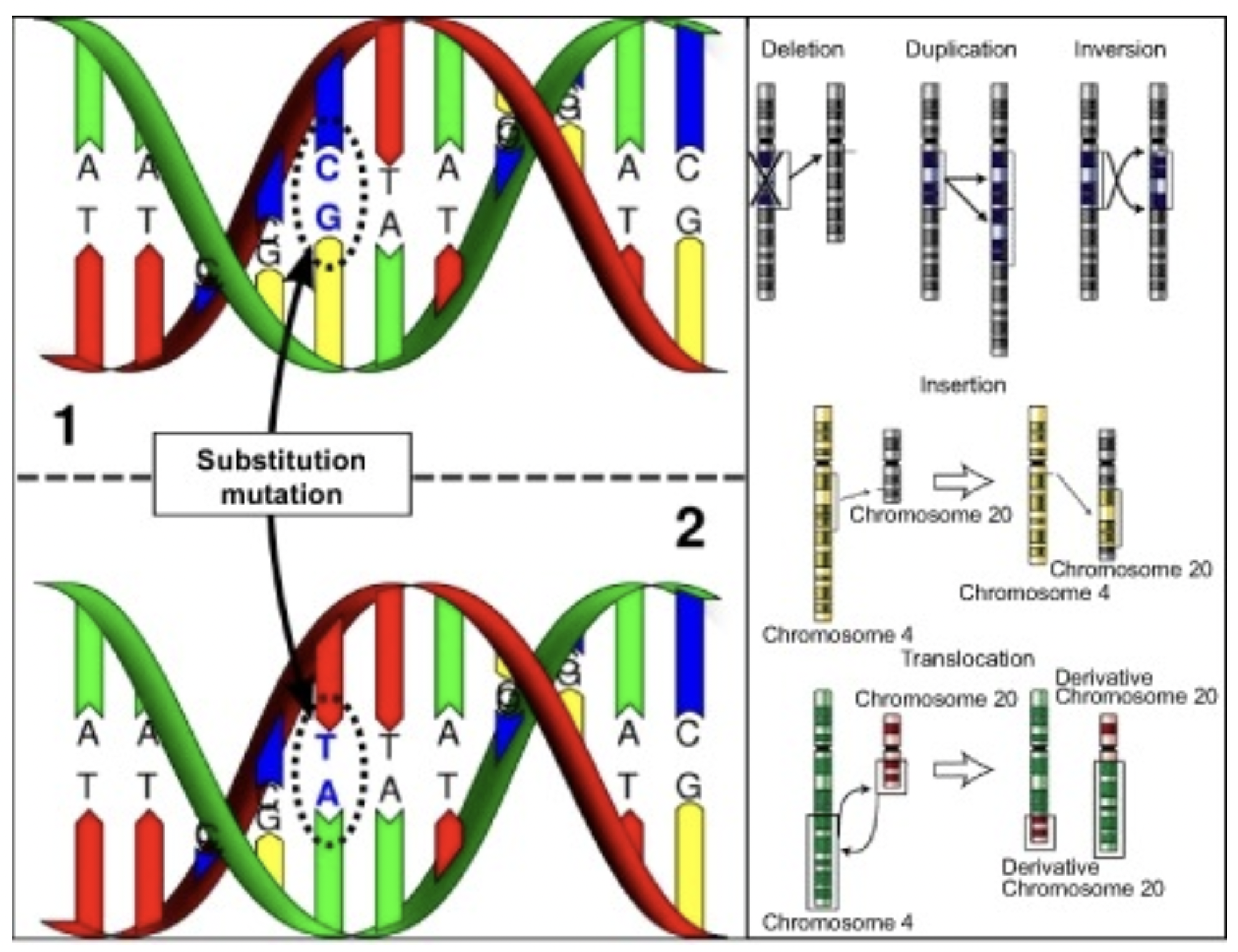
Genetic Variant Detection Over Generations: Sparsity-Constrained Optimization Using Block-Coordinate Descent
Mohammed Aburidi and Roummel Marcia
I introduced a novel approach -a constrained optimization method- to identify germline SVs by leveraging familial relationships within three generations of related individuals (a grandparent, a parent, and a child). We formulate this as a constrained optimization problem, employing sparsity-promoting penalties. Our framework demonstrates notable improvements in SV prediction accuracy among related individuals and effectively distinguishes true SVs from false positives. Evaluations on simulated and real genetic signals from the 1000 Genomes Project with low coverage confirm the efficacy of our approach. Additionally, our block-coordinate descent method not only delivers accurate results but also showcases the potential for application in more complex and higher-dimensional pedigrees, ensuring robustness and feasibility in varied genetic analyses.
Read less
Rubost Detrended Fluctuation Analysis (DFA) and its application to envelopes of human alpha rhythms
Mohammed Aburidi, Guido Nolte, Andreas K. Engel
L.
Read less
Reconstruction of the Spatio-temporal Activation Map of the Human Heart Voltage Evolution
Mohammed Aburidi, Hannah Love, Charles Rivera, Richard Tobing
L.
Read less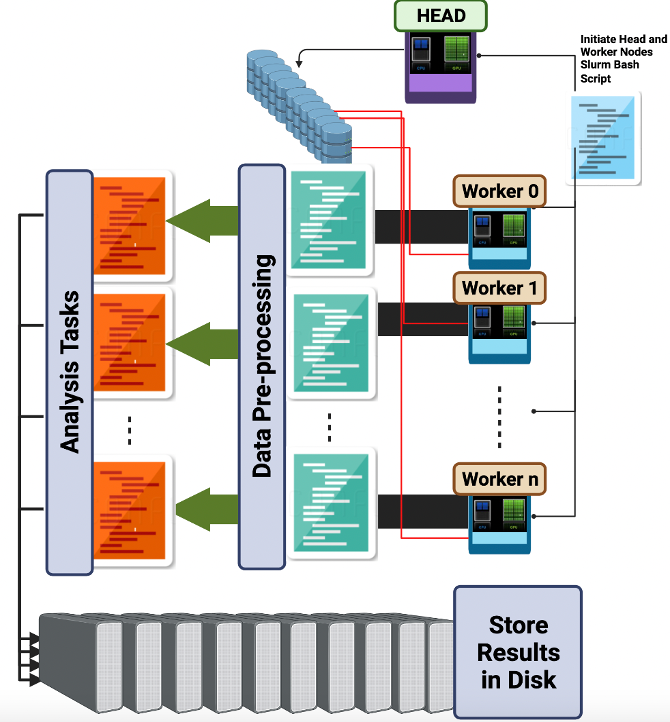
Parallelized Ray-Based Framework Adaptive ReaL Time Analysis of Big Fusion Data
Mohammed Aburidi, Laurie Stephey, Ralph Kube, Michael Churchill, Jong Choi
L.
Read less